What is Circular Function?
A Circular function can be defined in terms of an arc length and the coordinates of the terminal point of the arc on the unit circle.
In this topic, we'll focus on studying its 3 basic Circular Functions which are Sine (Sin), Cosine (Cos), and Tangent (Tan) functions, and their Reciprocal Functions which are Cosecant (Csc), Secant (Sec), and Cotangent (Cot) functions.
This is the image of the Unit Circle with angles in degree, radian measure, and their corresponding points in the circle.
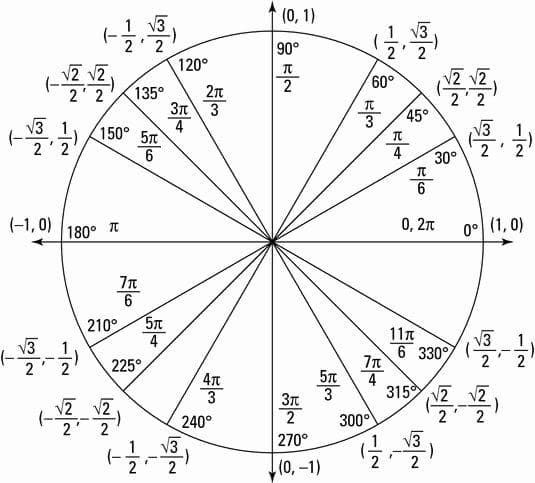
I SHOWED YOU THIS UNIT CIRCLE BECAUSE IN THIS TOPIC WE'RE GOING TO USE IT TO MAKE OUR WORK EASIER.
Moving Forward, Study these functions and observe which of them are partners!
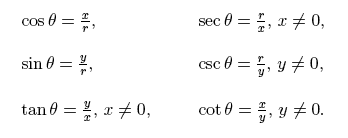
Remember! Cosine is the X, and Sine is the Y.
Have you absorbed all these things already? Now, let's keep on going!
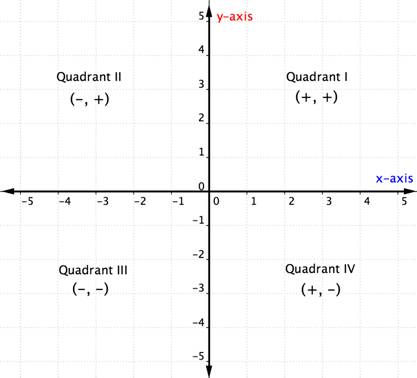
Knowing and understanding the 4 Quadrants are also important for this topic.
QUADRANT I 0° to 90°
QUADRANT II 91° to 180°
QUADRANT III 181°to 270°
QUADRANT IV 271° to 360°
Let's Start!
-In answering the given problems, you only have to be familiarize with the formula of the basic and reciprocal circular functions.
-Always remember that we can't also have a denominator of radicals on our answers. To eliminate them, just simply divide it to a radical value.EXAMPLES
ONCE YOU HAD THE X AND Y OR THE SINE AND COSINE, YOU CAN ALREADY EASILY FIND THE OTHER FUNCTIONS BY FOLLOWING THEIR FORMULA THAT WAS SHOWN ABOVE!
Still having a hard time absorbing all the given information? Here's a video for all of you!!
I KNOW YOU CAN DO IT! LET'S NOW LEARN AND VISIT THE NEXT TOPIC!!
Comments